Đề thi HSG Toán 9 thành phố Hà Nội năm 2020 – 2021

Đề thi HSG Toán 9 thành phố Hà Nội năm 2020

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI

KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 CẤP THÀNH PHỐ

Năm học 2020 – 2021
Môn thi : TOÁN
Ngày thi : 13/1/2021
Thời gian làm bài : 150 phút

Bài I (5,0 điểm)

1 ) Giải phương trình \ ( x ^ { 2 } – x + 8 = 4 \ sqrt { x + 3 } \ )
2 ) Cho a, b, c là những số thực đôi một khác nhau. Chứng minh biểu thức
\ ( K = \ dfrac { a ^ { 2 } } { ( a-b ) ( a-c ) } + \ dfrac { b ^ { 2 } } { ( b-a ) ( b-c ) } + \ dfrac { c ^ { 2 } } { ( c-a ) ( c-b ) } \ ) có giá trị nguyên .

Bài II ( 5,0 điểm)

1 ) Biết a, b, c là những số nguyên thỏa mãn nhu cầu a + b + c chia hết cho 3 và ab – bc – ca chia hết cho 3. Chứng minh ab – bc – ca chia hết cho 9 .
2 ) Cho đa thức \ ( P ( x ) = x ^ { 3 } + a x + b \ ) có nghiệm \ ( 1 + \ sqrt { 3 } \ ) ( a, b là những số hữu tỉ ). Chứng minh P ( x ) chia hết cho đa thức \ ( x ^ { 2 } – 2 x-2 \ )

Bài III (2,0 điểm) Với các số thực không âm a, b, c thỏa mãn \(a^{2}+b^{2}+c^{2}=1\), tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(Q=\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\).

Bài IV (6,0 điểm) Cho đường tròn (I) nội tiếp tam giác nhọn \(ABC (A B < A C)\). Đường tròn (I) tiếp xúc với BC, CA lần lượt tại D, E. Qua B kẻ đường thẳng vuông góc với BI, cắt AI tại J. Gọi P là hình chiếu vuông góc của J trên BC.

1 ) Chứng minh BD = CP .
2 ) Gọi N là giao điểm củaa hai đường thẳng AJ và BC. Chứng minh \ ( \ dfrac { 1 } { A I } + \ dfrac { 1 } { A J } = \ dfrac { 2 } { A N } \ ) .
3 ) Gọi Q. là giao điểm của hai đường thằng JP và DE. Gọi K là trung điểm của PQ. Chứng minh BK vuông góc với AP .

Bài V (2,0 điềm)

1 ) Tìm tổng thể những số nguyên dương x, y, z thỏa mãn nhu cầu \ ( 3 ^ { x } + 2 ^ { y } = 1 + 2 ^ { z } \ ) .
2 ) Cho một hình chữ nhật có diện tích quy hoạnh bằng 1. Năm điểm phân biệt được đặt tùy ý vào hình chữ nhật sao cho không có ba điểm nào thằng hàng ( mỗi điểm trong năm điểm đó hoàn toàn có thể được đặt trên cạnh hoặc đặt nằm trong hình chữ nhật ) .
a ) Chứng minh mọi tam giác tạo bởi ba trong năm điểm đã cho đều có diện tích quy hoạnh không vượt quá \ ( \ dfrac { 1 } { 2 } \ )
b ) Với mỗi cách đặt năm điểm vào hình chữ nhật như trên, gọi N là số tam giác có ba đỉnh là ba điểm trong năm điểm đó và có diện tích quy hoạnh không vượt quá \ ( \ dfrac { 1 } { 4 } \ ). Tìm giá trị nhỏ nhất của N .

Đáp án đề thi HSG Toán 9 thành phố Hà Nội năm 2020 – 2021

Bài I

1. Điều kiện xác lập : \ ( x \ geq-3 \ ). Phương trình khởi đầu tương tự với\ ( ( x-1 ) ^ { 2 } + ( \ sqrt { x + 3 } – 2 ) ^ { 2 } = 0 \ Longleftrightarrow x-1 = \ sqrt { x + 3 } – 2 = 0 \ Longleftrightarrow x = 1 \ )
Vậy S = 1
2. Quy đồng mẫu số biểu thức K thì ta được
\ ( K = \ frac { a ^ { 2 } ( c-b ) + b ^ { 2 } ( a-c ) + c ^ { 2 } ( b-a ) } { ( a-b ) ( b-c ) ( c-a ) } \ )
Phân tích thành nhân tử ở tử số của K
Tỷ số
\ ( K = a ^ { 2 } ( c-a+a-b ) + b ^ { 2 } ( a-c ) + c ^ { 2 } ( b-a ) \ \ = ( c-a ) \ left ( a ^ { 2 } – b ^ { 2 } \ right ) + ( a-b ) \ left ( a ^ { 2 } – c ^ { 2 } \ right ) \ \ = ( c-a ) ( a-b ) ( a + b ) + ( a-b ) ( a-c ) ( a + c ) \ \ = ( a-b ) ( c-a ) ( a + b-a-c ) \ \ = ( a-b ) ( b-c ) ( c-a ) \ )
Do vây, K = 1 \ ( \ in \ mathbb { Z } \ ) .

Bài II

1. Đặt a + b + c = 3 k ( với \ ( k \ in \ mathbb { Z } \ ) ). Khi đó ta có \ ( c = 3 k – ( a + b ) \ )

Vì vậy
\(a b-b c-c a =a b-c(a+b) \\ =a b-3 k(a+b)+(a+b)^{2} \\ =a^{2}+b^{2}+3 a b-3 k(a+b) .\)

Từ giả thiết ta suy ra \ ( a ^ { 2 } + b ^ { 2 } \ ) chia hết cho 3. Sử dụng hiệu quả quen thuộc ta suy ra a, b đều chia hết cho 3, điều này cũng kéo theo c chia hết cho 3 .
Như vậy, ab – bc – ca chia hết cho 9

2. Ta có \(P(1+\sqrt{3})=0\) nên \((1+\sqrt{3})^{3}+a(1 \sqrt{3})+b=0\) hay

\ ( ( a + b + 10 ) + ( a + 6 ) \ sqrt { 3 } \ )= 0Vì a, b là những số hữu tỉ nên a + b + 10, a + 6 cũng là những số hữu tỉ nên theo tác dụng suy ra \ ( a + b + 10 = a + 6 = 0 \ ). Khi đó \ ( P ( 1 – \ sqrt { 3 } ) = ( a + b + 10 ) – ( a + 6 ) \ sqrt { 3 } = 0 \ ) .
Điều này có nghĩa là P ( x ) có nghiệm là \ ( 1 – \ sqrt { 3 } \ ). Suy ra P ( x ) chia hết cho \ ( ( x – ( 1 + \ sqrt { 3 } ) ) ( x – ( 1 – \ sqrt { 3 } ) ) = x ^ { 2 } – 2 x-2 \ )

Bài III

1. Vì \ ( ( a + b + c ) ^ { 2 } \ leq 3 \ left ( a ^ { 2 } + b ^ { 2 } + c ^ { 2 } \ right ) = 3 \ ) nên \ ( a + b + c \ leq \ sqrt { 3 } \ ). Áp dụng bất đẳng thức Bunhiacovsky, ta có
\ ( Q ^ { 2 } \ leq 3 ( a + b + b + c + c + a ) = 6 ( a + b + c ) \ leq \ sqrt { 108 } \ )
nên \ ( Q \ leq \ sqrt [ 4 ] { 108 } \ ). Dấu bằng xảy ra khi và chỉ khi \ ( a = b = c = \ frac { 1 } { \ sqrt { 3 } } \ ). Từ đó giá trị lớn nhất của Q. là \ ( \ sqrt [ 4 ] { 108 } \ ) .
2. Từ giả thiết suy ra \ ( a, b, c \ leq 1 \ ) kéo theo \ ( a \ geq a ^ { 2 }, b \ geq b ^ { 2 }, c \ geq c ^ { 2 } \ ) .
Ta có
\ ( Q ^ { 2 } = 2 ( a + b + c ) + 2 \ sqrt { ( a + b ) ( a + c ) } + 2 \ sqrt { ( b + c ) ( b + a ) } + 2 \ sqrt { ( c + a ) ( c + b ) } \ )
và quan tâm là \ ( ( a + b ) ( a + c ) \ geq a ^ { 2 }, \ ldots \ ) nên \ ( Q ^ { 2 } \ geq 4 ( a + b + c ) \ geq 4 \ left ( a ^ { 2 } + b ^ { 2 } + c ^ { 2 } \ right ) = 4 \ ) .
Suy ra \ ( Q \ geq 2 \ )
Dấu bằng xảy ra ví dụ điển hình khi a = 1, b = c = 0. Vây giá trị nhỏ nhất của Q. là 2 .

Bài IV

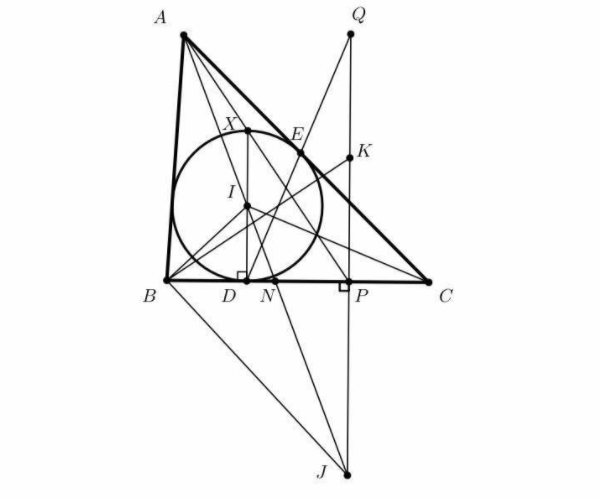
1. Từ giả thiết ta suy ra J là tâm của đường tròn ( J ) bàng tiếp đỉnh A của tam giác ABC và P là tiếp điểm của đường tròn ( J ) với cạnh BC. Đặt BC = a, CA = b, AB = c và \ ( p = \ frac { a + b + c } { 2 } \ ). Từ tác dụng quen thuộc thì ta có
\ ( BD = CP = p-b = \ frac { A B + B C-C A } { 2 } \ )
2. 2. Ta có BI, BJ tương ứng là phân giác trong và phân giác ngoài của \ ( \ widehat { A B C } \ ). Sử dụng đặc thù phân giác cho tam giác ABN thì ta được
\ ( \ frac { A N } { A I } = \ frac { B A + B N } { B A } \ ) và \ ( \ frac { A N } { A J } = \ frac { B A-B N } { B A } \ )
Do đó, \ ( \ frac { A N } { A I } + \ frac { A N } { A J } = 2 \ ) Từ đó suy ra \ ( \ frac { 1 } { A I } + \ frac { 1 } { A J } = \ frac { 2 } { A N } \ )
3. Dựng đường kính DX của đường tròn ( I ). Ta có hiệu quả quen thuộc rằng A, X, P thẳng hàng. Chú ý rằng ta có \ ( C I \ perp D E \ )
Do \ ( \ widehat { D I C } = \ widehat { P D Q } \ left ( = 90 ^ { \ circ } – \ widehat { I C B } \ right ) \ ) nên \ ( \ triangle I D C \ sim \ triangle D P Q ( g. g ). \ )
Từ đó suy ra \ ( \ frac { D P } { P Q } = \ frac { I D } { C D } = \ frac { I D } { B P } \ ) .
Để ý rằng DX = 2 ID và PQ = 2PK, nên ta được
\ ( \ frac { D P } { P K } = \ frac { 2 D P } { P Q } = \ frac { 2 I D } { B P } = \ frac { D X } { B P } \ )
Điều này kéo theo \ ( \ triangle D P X \ sim \ triangle P K B ( \ mathrm { c. g. c } ) \ ) .
Do dó, \ ( \ widehat { A P B } = \ widehat { X P D } = \ widehat { B K P } = 90 ^ { \ circ } – \ widehat { P B K } \ )
hay \ ( \ widehat { A P B } + \ widehat { P B K } = 90 ^ { \ circ } \ ) .
Vì vậy, \ ( B K \ perp A P \ )

Bài V

1. Ta có \ ( 1 + 2 ^ { z } = 3 ^ { x } + 2 ^ { y } > 2 ^ { y } \ ) nên \ ( z > y \ ). Ngoài ra vì \ ( 2 ^ { y } – 2 ^ { z } \ equiv 1 ( \ bmod 3 ) \ ) nên z chẵn, còn y lẻ .
Xét những năng lực
( a ) Nếu y = 1 thì \ ( 3 ^ { x } = 2 ^ { z } – 1 = \ left ( 2 ^ { k } – 1 \ right ) \ left ( 2 ^ { k } + 1 \ right ) \ ) với \ ( k = \ frac { z } { 2 } \ ) .
Vì \ ( \ left ( 2 ^ { k } + 1 \ right ) – \ left ( 2 ^ { k } – 1 \ right ) = 2 \ ) không chia hết cho 3 nên \ ( 2 ^ { k } – 1 = 1 \ ) kéo theo k = 1 .
Từ đó tìm được z = 2, x = 1 .
Suy ra ( x, y, z ) = ( 1 ; 1 ; 2 ) là một nghiệm của phương trình đã cho .

” Lời giải đề thi chọn học viên giỏi lớp 9 môn Toán, thành phố Hà Nội năm học 2020 – 2021, được triển khai bởi những thành viên của Tổ Kiến ( Câu lạc bộ Toán A1 ). ”
– / –
Trên đây là đề thi HSG Toán 9 thành phố Hà Nội năm 2020 – 2021 do Đọc tài liệu tổng hợp, mong rằng với nội dung này sẽ giúp những em ôn tập kỹ năng và kiến thức thi cuối kì 1 tốt hơn. Đừng quên còn trọn bộ đề thi thử vào 10 môn Toán qua những năm đang đợi những em giải đáp .

Source: https://hanoittfc.com.vn
Category: Dịch Vụ